4. Work, energy and momentum

A particle is moving from point $A$ to $B$ along the path shown below. The movement is due to a force $\overrightarrow{F}$ which is acting along an angle of $\theta$ with the infinitesimal displacement vector $d\overrightarrow{r}$.

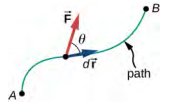
The infinitesimal work done by this particle for a displacement of $d\overrightarrow{r}$ can be written as

$$ dW = \overrightarrow{F} \cdot d\overrightarrow{r} = F dr \cos\theta. $$

So work is dot product between force and displacement. Work is maximum when the angle between the force and displacement is $0^\circ$, that is when those are in the same direction. Work is minimum when this angle is $90^\circ$, that is when displacement is perpendicular to the displacement.

If $\overrightarrow{F}=F_x\hat{i}+F_y\hat{j}$ and $d\overrightarrow{r}=dx\hat{i}+dy\hat{j}$, then

$$ dW = \overrightarrow{F} \cdot d\overrightarrow{r} = F_x dx + F_y dy $$

where we have used the vector relation $\overrightarrow{A} \cdot \overrightarrow{B} = A_x B_x + A_y B_y$. Integrating both sides we get

$$ W = \int_A^B \overrightarrow{F} \cdot d\overrightarrow{r}, $$

which means that the total work done by a force is the integral of the force with respect to displacement along the path of the displacement.

Work is always done by a force. The unit of work (J, joule) can be derived from the units of force (N) and displacement (m):

$$ 1 \text{ J} = 1 \text{ N m} = 1 \text{ kg} \text{ m}^2 \text{ s}^{-2}. $$

Meaning of work in physics is very different from the everyday meaning of work. If I am standing still with a 20-kg load on my back, I am doing no work because the displacement is zero.

If the force does not depend on displacement, if it is the same at every point along a path, then the integral becomes simpler. Take force out of the integral and write

$$ W = \overrightarrow{F} \cdot \int_A^B d\overrightarrow{r} = F (r_B-r_A) \cos\theta = F \Delta r \cos\theta. $$

Several forces are usually considered to be constant or almost constant.

A moving car has a normal force exerted on it by the road. The normal force ($N$) is perpendicular to the displacement or the motion of the car, so it does no work; for a displacement of $\Delta r$ the work done by normal force $W_N = N \Delta r \cos(90^\circ) = 0$.

Frictional force $f$ is always opposite to the direction of motion. So work done by friction is negative: $W_f = f \Delta r \cos(180^\circ) = -f\Delta r$.

Work done by gravity can also be discussed here. Gravitational force or weight ($\mathbf{w}$) is approximated to be constant near the surface of the earth. So work done by gravity when something moves from a height $y_A$ to $y_B$ can be written as

$$ W_g = w (y_B-y_A) \cos(0^\circ) = mg \Delta y. $$

The integral can be simple even when the force is not constant but a simple function of position. The restoring force exerted by a spring on a block attached to it is $F=-kx$ where $k$ is the spring constant and $x$ the position of the block with respect to the equilibrium position $x=0$. So the work done by the elastic restoring force of a spring

$$ W_e = \int_A^B F_x dx = -k \int_A^B x dx = -\frac{1}{2}k(x_B^2-x_A^2).$$

We can understand work geometrically as well. Integration is related to the area under a curve as we discussed in Chapter 2. If we plot force as a function of displacement, the area under the line or curve describing the force will be the work.

The straight line gives the force as a function of position. They are opposite to each other as we know that $F\propto -x$. The shaded area under or above the line up to the $x$-axis is the work done by the spring for a particular displacement.

There is an energy associated with motion. Otherwise a moving thing could not put another thing into motion.

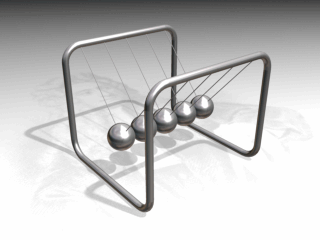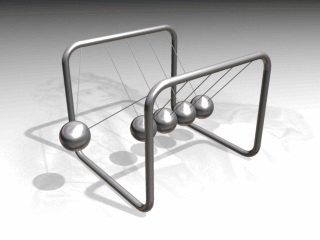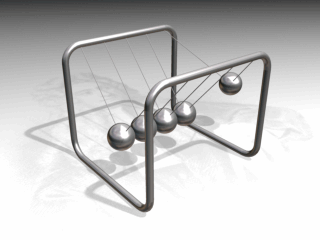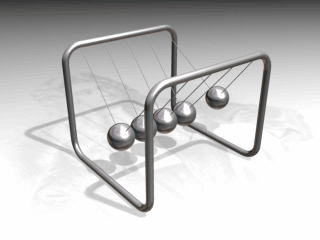
In the Newton’s cradle shown above, the energy of the first swinging sphere is transferred all the way to the last sphere. This is the kinetic energy. The kinetic energy of an object or system of mass $m$ moving with a speed of $v$ is given as

$$ K = \frac{1}{2}mv^2 $$

which is a scalar. There is another quantity which depends only on mass and velocity but which is a vector. It is called momentum, mathematically

$$ \overrightarrow{p} = m\overrightarrow{v}. $$

The equations show the units. The unit of kinetic energy or any energy is J (joule), the same as the unit of work. Sometimes energy is defined as the ability to do work. The equation $K=mv^2/2$ indeed gives the unit kg m$^2$ s$^{-2}$ which is equivalent to J.

The unit of momentum, on the other hand is (according to the definition above) kg m s$^{-1}$.

Kinetic energy can be expressed in terms of the magnitude of the momentum vector:

$$ K = \frac{p^2}{2m}. $$

The units already gave away the relationship between work and energy. Here we derive it using the definition of work and Newton’s second law of motion. Infinitesimal work

$$ dW = \mathbf{F} \cdot d\mathbf{r} = m \frac{d\mathbf{v}}{dt} \cdot d\mathbf{r} = m \mathbf{v} \cdot d\mathbf{v} = m(v_xdv_x+v_ydv_y) $$

where we have used Newton’s second law ($\mathbf{F}=m\mathbf{a}$). Now integrating this we get

$$ W = \frac{1}{2}m \int_A^B (v_x^2+v_y^2) = \frac{1}{2}m (v_B^2-v_A^2) = K_B - K_A = \Delta K $$

which means work is the difference in kinetic energy. When something moves from point $A$ to $B$, the force responsible for the displacement does some work and the kinetic energy of the thing changes as a result. The work is directly equal to that change:

$$ W = \Delta K. $$

Consider a 60-kg sprinter starting from rest ($v=0$) and reaching a speed of 2 m/s after 1 min. Her initial kinetic energy $K_i$ is zero and the final kinetic energy $K_f=mv^2/2=4$ J. That automatically means she has done $\Delta K=K_f-K_i=4$ J of work in that 1 minute.

Neither work nor energy cares about time. Their equations to not have time. Power remedies that. Power is nothing but the rate at which work is done. Power is a derivative of work with respect to time.

$$ P = \frac{dW}{dt} = \frac{d}{dt} (\mathbf{F} \cdot d\mathbf{r}) = \mathbf{F} \cdot \frac{d\mathbf{r}}{dt} = \mathbf{F} \cdot \mathbf{v}. $$

Compare the final form of the equation with the definition of work. What displacement is to to work, velocity is to power. Power is the dot product of the force and velocity vectors.

Unit of work would obviously be J s$^{-1}$ or W (watt).

Kinetic energy is related to the intrinsic velocity and mass of an object. But there is another form energy, the potential energy, which depends not on the velocity but on the position of an object (or system) with respect to another object or system.

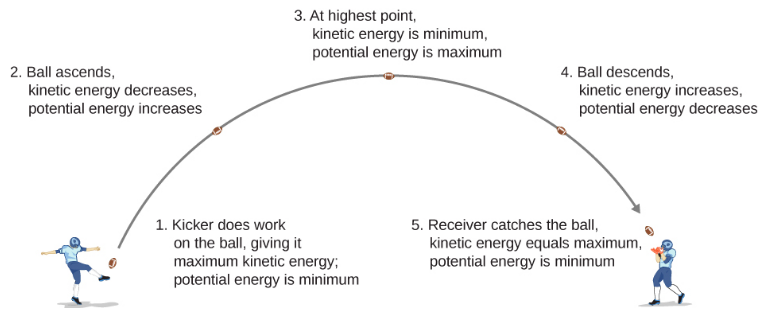
Consider the throwing of a baseball as shown above. Initially the ball had kinetic energy $K$ which is completely converted to potential energy $U$ at the maximum height and then this $U$ is converted back to $K$ as the ball comes back down. The ball gains potential energy because its position with respect to the most massive object around (the earth) is changes.

As the ball goes from the ground (point $A$) to the maximum height (point $B$) its change in kinetic energy $\Delta K = K_f-K_i=-K_i$ and its change in potential energy $\Delta U = U_f-U_i=U_f$. As $K_i$ is completely converted to $U_f$, it must be the case that $U_f = K_i$. That would mean $\Delta U = -\Delta K$. So the work energy theorem can be re-written as

$$ W = \Delta K = -\Delta U. $$

This is a statement of the conservation of energy as we will see later. Potential energy is defined always with respect to a reference point because it is a relational quantity. By definition

$$ \Delta U_{AB} = U(\mathbf{r}) - U(\mathbf{r}_0) $$

where $U(\mathbf{r})$ is the potential energy at $\mathbf{r}$ with respect to the reference position $\mathbf{r}_0$.

We have calculated the work done by gravitational and elastic forces. Every force has an associated potential energy because force is the influence of a particular object or system and any other object or system located within that sphere of influence would have a potential energy. We can calculate potential energy from work.

Gravitational potential energy $\Delta U_g = -W_g = mg(y_B-y_A) = mgh = mgy$ where height $h=y=y_B-y_A$. You see that the definition of potential energy is hidden in this very equation:

$U_g = mgh$

where $m$ belongs to the object for which we are calculating the energy, $g$ is property of the earth within whose force-field the object is located and $h$ is a property of both the object and the earth.

On the other hand, elastic potential energy

$$ \Delta U_e = -W_e = \frac{1}{2}k(x_B-x_A)^2. $$

Think of a system that combines this two potential energies: a vertical spring.

In a vertical spring the block goes down because of its weight or gravitational force and comes back up because of the elastic restoring force of the spring.

Based on the discussions of kinetic and potential energy we saw that (in case of a baseball throw)

$$ \Delta K = - \Delta U \Rightarrow \Delta U + \Delta K = 0 \Rightarrow \Delta E = 0 $$

or the total energy of the system $E=K+U$ does not change, as $\Delta E=0$. This is the law of conservation of energy, THE most fundamental law in physics. It can be written using calculus more appropriately if we change the $\Delta$ into $d$ and write:

$$ \frac{dE}{dt} = 0 $$

or the rate of change of energy within any closed system is zero which would automatically mean

$$ E = constant. $$

Note that $E$ here is the total energy of a closed system, a system that does not interact with its surroundings.

But of course most systems are not closed, they always interact. We can rewrite the conservation of energy by remembering the work-energy theorem and write that the work done by non-conservative forces

$$ W_{nc} = \Delta K + \Delta U = \Delta E. $$

In case of the baseball above, $W_{nc}$ is the work done by friction which is a non-conservative force. If we ignore the friction due to air resistance, if all work is done by only by conservative forces, then

$$ W_{nc} = \Delta K + \Delta U = \Delta E = 0 $$

which is the first form of the law of conservation of energy we saw before. This law is related to the law of conservation of momentum and Newton’s second and third laws of motion in curious ways which will be clear later.

This graph shows the potential ($U$, blue), kinetic ($K$, red) and total ($E$, green) energies as a function of time for the baseball. The position of the baseball can be modelled as a sine wave, $U$ is related to position, so the $U-t$ curve is a sine curve. But kinetic energy is related to velocity, the derivative of position, and hence the $K-t$ curve is a cosine curve. The total energy is a straight line as it never changes. At each point in time $E=K+U$.

You already encountered momentum, but here we discuss it in more detail and try to see the mysterious analogy between momentum and work.

The magnitude of momentum ($p=mv$) can be more or less than magnitude of velocity depending on the mass of the object or system. But the direction of momentum is always toward the direction of velocity. Mass, a scalar, cannot change the direction of a vector.

We get work by combining the concept of force and displacement. And we get a new quantity, called the impulse, by combining the concepts of force and time. When a force $F$ is exerted on an object or system for an infinitesimally small amount of time $dt$, the impulse

$$ d\mathbf{J} = \mathbf{F} dt = m \mathbf{a} dt $$

What space is to work ($dW=\mathbf{F} \cdot d\mathbf{r}$), time is to impulse. If the force is exerted from time $t_i$ to $t_f$, then the total impulse during this period

$$ \mathbf{J} = \int_{t_i}^{t_f} \mathbf{F} dt = m \int_{t_i}^{t_f} \mathbf{a} dt = m(\mathbf{v}_f-\mathbf{v}_i) = m\Delta\mathbf{v} = \Delta\mathbf{p} $$

which brings us back to the work-energy theorem. Just as work is equal to the change in kinetic energy, so impulse is equal to the change in momentum. The first is a scalar relationship and the second a vector relationship. Let us express the second case again because it is extremely important:

$$ \overrightarrow{J} = \Delta \overrightarrow{p} $$

which is also called the impulse-momentum theorem.

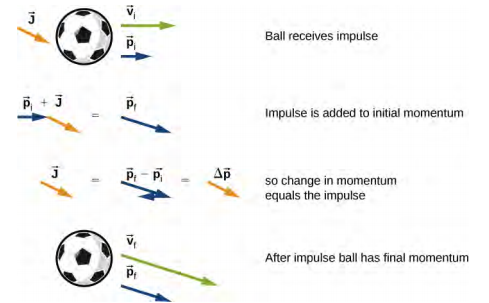
The theorem is graphically explained above. The football receives a kick (a force) for a certain period of time (maybe less than a second) and its momentum changes as a result. The impulse is exactly equal to the change in momentum.

The unit of impulse would obviously be N s (unit of work is N m).

Just as the total energy of a closed system can never change, it turns out the total momentum of a closed system can also never change. What do we mean by a system? A system is a collection of things. The system is closed if that collection is completely isolated from its surrounding.

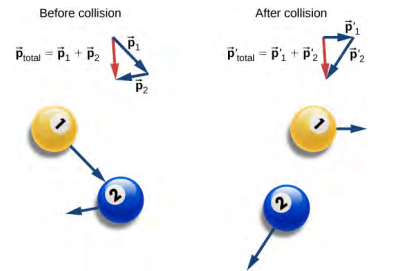
Let us consider a system that has just two billiard balls. The total initial momentum of the system is the sum of the momentums of the two balls ($\overrightarrow{p}_1$ and $\overrightarrow{p}_2$). Now $\overrightarrow{p}_1$ and $\overrightarrow{p}_2$ can change as much as they want but their sum $\overrightarrow{p}=\overrightarrow{p}_1+\overrightarrow{p}_2$ will always be the same unless the system interacts with its environment, unless the an external force is applied on the system.

This is called the law of conservation of momentum and, similar to the law of conservation of energy, it can be expressed as

$$ \frac{d\overrightarrow{p}}{dt} = 0 $$

which amounts to saying that $\overrightarrow{p}$ is a constant. This law can be proved using the momentum form of Newton’s second law of motion which says that the next external force on a system

$$ \mathbf{F} = \frac{d\mathbf{p}}{dt}. $$

Now if there is no net external force on a system, $\mathbf{F}=0$ and so $\frac{d\mathbf{p}}{dt}=0$. By the way compare the above equation with the equation expressing the conservation of energy above. You see that what net external force is doing in case of the conservation of momentum, the net work done by non-conservative forces is doing in case of the conservation of energy. This is an interesting similarity.

By the way, when net external force is zero, Newton’s second law becomes the first law. So Newton’s first law is actually an expression of the conservation of linear momentum for a closed system.

And it turns out Newton’s third law if also an expression of the law of conservation of momentum. Let us prove this using the billiard ball example described above. Ball 1 exerts a force ($\mathbf{F}_{12}$) on Ball 2 and Ball 2 exerts and equal and opposite force ($F_{21}$) on Ball 1. So

$$ \mathbf{F}_{12} = - \mathbf{F}_{21} \Rightarrow m_2\mathbf{a}_2 = -m_1\mathbf{a}_1 \Rightarrow m_1\frac{d\mathbf{v}_1}{dt} = - m_2\frac{d\mathbf{v}_2}{dt} = 0. $$

But here mass is a constant and can be brought within the derivative. So we get

$$ \frac{d}{dt}(m_1\mathbf{v}_1) + \frac{d}{dt}(m_2\mathbf{v}_2) = 0 \Rightarrow \frac{d}{dt}(\mathbf{p}_1+\mathbf{p}_2) = \frac{d\mathbf{p}}{dt} = 0 $$

which is nothing but the law of conservation of linear momentum for a closed system.

This is a curious development: the three laws of Newton are nothing but different expressions of the law of conservation of momentum?

The concept of center of mass is extremely important because we cannot do any calculation of motion without first defining a center of a system with respect of which all change in position or velocity should be measured. Center of mass has to be defined using Newton’s second law: $\mathbf{F}=M\mathbf{a}$. Here $\mathbf{F}$ is the net external force of a system, $M$ the total mass of the system and $\mathbf{a}$, the net acceleration of the system.

But what do we mean by the acceleration of a system. Acceleration is rate of change of velocity, velocity is rate of change of position, but position has to be measured from a particular point. Which point within an extended system should be taken as the origin for measuring position or displacement? Answer: center of mass. So $\mathbf{a}$ is the acceleration of the center of mass of the system. Let us write $\sum \mathbf{F}_{ext}=M\mathbf{a}_{cm}$. But remembering the momentum form of the second law of the definition of using momentum, we can write

$$ M\mathbf{a}_{cm} = \frac{d\sum \mathbf{p}}{dt} $$

where $\sum \mathbf{p}$ is the total momentum of the system. If there are many particles in the system, and the $i$-th particle has mass $m_i$, velocity $\mathbf{v}_i$ and position $\mathbf{r}_i$, then

$$ M\mathbf{a}_{cm} = \frac{d}{dt} \sum_i m_i\mathbf{v}_i = \frac{d}{dt} \sum_i m_i\frac{d\mathbf{r}_i}{dt} = \frac{d^2}{dt^2} \sum_i m_i\mathbf{r}_i $$

which means that the acceleration of the center of mass

$$ \mathbf{a}_{cm} = \frac{d^2}{dt^2} \left(\frac{1}{M}\sum_i m_i\mathbf{r}_i\right) = \frac{d^2\mathbf{r}_{cm}}{dt^2} $$

where we have used the definition of center of mass

$$ \mathbf{r}_{cm} = \frac{1}{M}\sum_i m_i\mathbf{r}_i. $$

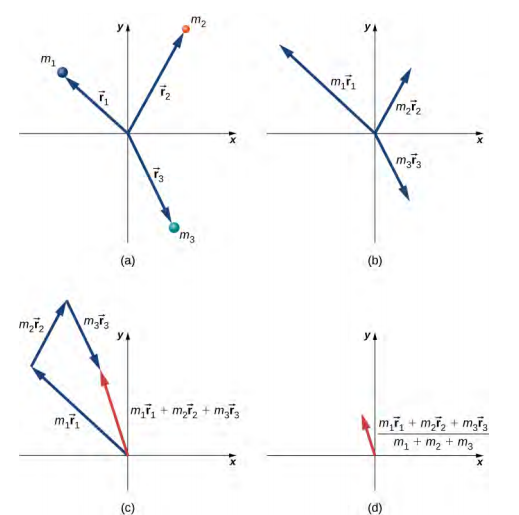
The diagram shows an illustration of this $\mathbf{r}_{cm}$ for a system with three particles. For three particles

$$ \mathbf{r}_{cm} = \frac{1}{M} \sum_{i=1}^{3} m_i\mathbf{r}_i = \frac{m_1\mathbf{r}_1 + m_2\mathbf{r}_2 + m_3\mathbf{r}_3}{m_1+m_2+m_3}. $$