Problems

Ultrasound machines are used by medical professionals to make images for examining internal organs of the body. An ultrasound machine emits high-frequency sound waves, which reflect off the organs, and a computer receives the waves, using them to create a picture. We can use the formulas presented in this module to determine the frequency, based on what we know about oscillations. Consider a medical imaging device that produces ultrasound by oscillating with a period of 0.400 $\mu$s. What is the frequency of this oscillation?

Period $T=0.4$ $\mu$s. So frequency

$$ f = \frac{1}{T} = \frac{1}{0.4\times 10^{-6}} = 2.5\times 10^6. $$

Answer: frequency of the ultrasound is 2.5 MHz.

Significance: Human audible range is 20 Hz to 20 kHz. So we cannot hear this sound.

A $2$-kg block is placed on a frictionless surface. A spring with a force constant of $k = 32$ N/m is attached to the block, and the opposite end of the spring is attached to the wall. The spring can be compressed or extended. The equilibrium position is marked as $x = 0$ m. Work is done on the block, pulling it out to $x = + 0.02$ m. The block is released from rest and oscillates between $x = + 0.02$ m and $x = −0.02$ m. Determine the equations of motion.

Equations of motion are nothing but the equations for position $x(t)$, velocity $v(t)$ and acceleration $a(t)$.

$$ x(t) = A \cos \omega t. $$ $$ v(t) = -\omega A\sin \omega t. $$ $$ a(t) = -\omega^2 A \cos \omega t. $$

We ignored phase angle $\phi$ because the block starts from maximum distance $+0.02$ m at time $t=0$ thereby making $\phi=0$.

Here $\omega$ and $A$ are the only unknown constants. $A$ is given as 0.02 m. And the angular frequency

$$ \omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{32}{2}} = 4 \text{ rad/s}. $$

So the equations of motion become

$$ x(t) = 0.02 \cos (4 t). $$ $$ v(t) = - 0.08 \sin (4 t). $$ $$ a(t) = - 0.32 \cos (4 t). $$

What is the acceleration due to gravity in a region where a simple pendulum having a length 75.000 cm has a period of 1.7357 s?

The angular frequency of a simple pendulum $\omega=\sqrt{g/L}$, so its period $T=2\pi\sqrt{L/g}$. Hence acceleration due to gravity

$$ g = 4\pi^2\frac{L}{T^2} = 4\pi^2\frac{0.75000}{(1.7357)^2} = 9.8281.$$

In extreme conditions, skyscrapers can sway up to two meters with a frequency of up to 20 Hz due to high winds or seismic activity. Several companies have developed physical pendulums that are placed on the top of the skyscrapers. As the skyscraper sways to the right, the pendulum swings to the left, reducing the sway. Assuming the oscillations have a frequency of 0.50 Hz, design a pendulum that consists of a long beam, of constant density, with a mass of 100 metric tons and a pivot point at one end of the beam. What should be the length of the beam?

The equation describing the oscillation of a physical pendulum:

$$ I\alpha = \tau \Rightarrow I \frac{d^2\theta}{dt^2} = -L mg\sin\theta \Rightarrow \frac{d^2\theta}{dt^2} = -\frac{mgL}{I} \theta $$

where we have used the small angle approximation $\sin\theta\approx \theta$. Here $L$ is the length of the pendulum. By analogy with the equation of simple harmonic motion $d^2x/dt^2=-kx/m$, the angular frequency of the physical pendulum

$$ \omega = \sqrt{\frac{mgL}{I}} \Rightarrow T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{I}{mgL}} $$

where $T$ is the period. The moment of inertia of a thin rod rotating with an axis through one end $I=mL^2/3$ where $m$ is the mass of the rod. Therefore

$$ T = 2\pi \sqrt{\frac{mL^2/3}{mgL}} = 2\pi \sqrt{\frac{L}{3g}} $$

$$ \Rightarrow L = 3g\left(\frac{T}{2\pi}\right)^2 = 3g\left(\frac{1}{2\pi f}\right)^2 $$

where frequency $f=0.5$ Hz. So the length $L = 2.98$ m. If $L$ is the length of the pendulum, the length of the beam

$$ L_B = 2L = 5.96 \text{ m}. $$

One half of the beam rotates with respect to the center of mass of the beam. The other half is vertically fixed to the roof.

A student takes a 30-m-long string and attaches one end to the wall in the physics lab. The student then holds the free end of the rope, keeping the tension constant in the rope. The student then begins to send waves down the string by moving the end of the string up and down with a frequency of 2 Hz. The maximum displacement of the end of the string is 20 cm. The first wave hits the lab wall 6 s after it was created.

a) What is the speed of the wave?
b) What is the period of the wave?
c) What is the wavelength of the wave?

a) The wave traveled 30 m in 6 s, so the wave speed $v=30/6=5$ m/s.

b) The frequency of the wave is the same as the frequency of the vertical oscillation and the period is the inverse of the frequency. So the period $T=1/f=1/2=0.5$ s.

c) The wavelength $\lambda=vT=5\times 0.5=2.5$ m.

A transverse mechanical wave propagates in the positive x-direction through a spring (as shown below) with a constant wave speed, and the medium oscillates between +A and −A around an equilibrium position.

The graph shows the height of the spring (y) versus the position (x), where the x-axis points in the direction of propagation. The figure shows the height of the spring versus the x-position at t = 0.00 s as a dotted line and the wave at t = 3.00 s as a solid line.

a) Determine the wavelength and amplitude of the wave.
b) Find the propagation velocity of the wave.
c) Calculate the period and frequency of the wave.

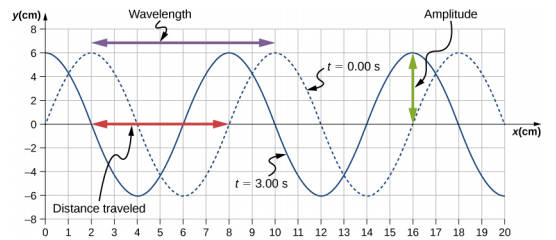
a) According to the graph, wavelength $\lambda=10-2=8$ cm (violet arrow) and the amplitude $A=6$ cm (green arrow).

b) According to the graph, the wave has traveled by $8-2=6$ cm in 3 s. So its speed $v=6/3=2$ cm/s.

c) Period $T=\lambda/v=8/2=4$ s. And frequency $f=1/T=1/4=0.25$ Hz.

A transverse wave on a taut string is modeled with the wave function

$$ y(x,t) = A \sin(kx-\omega t) = 0.2 \sin(6.28x-1.57t). $$

Find the amplitude, wavelength, period and speed of the wave.

By comparing the equations, we find amplitude $A=0.2$ m. [As no units are given in the equation, we are assuming everything to be in SI units.]

Wave number $k=2\pi/lambda=6.28$ m$^{-1}$. So wavelength $\lambda=2\pi/6.28=1$ m.

Angular frequency $\omega=2\pi/T=1.57$ s$^{-1}$. So period $T=2\pi/1.57=4$ s.

Speed of the wave $v=\lambda/T=1/4=0.25$ m/s. Or, equivalently, $v=\omega/k=1.57/6.28=0.25$ m/s.