Table of Contents
M2. Compound pendulum
Determining the value of gravitational acceleration ($g$) using a compound pendulum.
Theory

$$ \tau = -mgl \sin\theta = -mgl\theta. $$
$$ \tau = I \frac{d^2\theta}{dt^2} $$
$$ \tau = -mgl \sin\theta = -mgl\theta. $$
$$ \frac{d^2\theta}{dt^2} = - \frac{mgl}{I} \theta $$
$$ T_c = 2\pi\sqrt{\frac{I}{mgl}} $$
$$ I = I_G + ml^2 = mK^2 + ml^2 $$
$$ T_c = 2\pi\sqrt{\frac{mK^2+ml^2}{mgl}} = 2\pi\sqrt{\frac{\frac{K^2}{l}+l}{g}} $$
Compare this with the period of a simple pendulum
$$ T_s = 2\pi\sqrt{\frac{L}{g}} $$
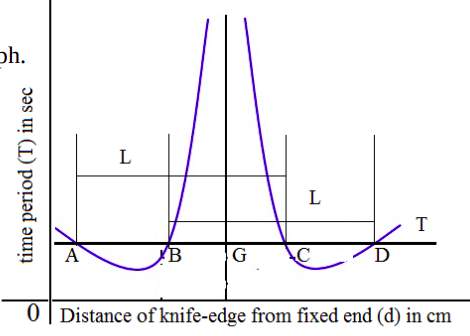
Comparing $T_c$ and $T_s$,
$$ L = \frac{K^2}{l}+l \Rightarrow l^2 - lL + K^2 = 0. $$
This equation has two solutions $l_1$ and $l_2$ where $L=l_1+l_2$ and $K=\sqrt{l_1l_2}$.