Bounce Motion

While discussing the concept of the adiabatic invariant, we saw that particles gyrating due to a magnetic mirror get reflected. In this case, the pitch angle of the gyration satisfies the relationship:

$$ \sin\alpha = \sqrt{\frac{B}{B_m}} $$

where \( B_m \) is the magnetic field strength at the mirror point (the point of reflection for the particle). For a magnetic dipole field, the magnetic field strength is minimum at the equator, where the magnetic latitude \( \lambda = 0 \). Therefore, at the point where a field line intersects the Earth’s equatorial plane, the ‘equatorial’ pitch angle is given by:

$$ \sin^2\alpha_{eq} = \frac{B_{eq}}{B_m}; $$

Here, \( B_{eq} = \frac{B_E}{L^3} \), where \( B_E \) is the magnetic field strength at the Earth’s surface, and \( L \) is the field line’s L-value. This equation can be derived by substituting \( \lambda = 0 \) into the magnetic dipole field equations. Substituting the magnetic field strength at the mirror point into the above equation yields:

$$ \sin\alpha_{eq} = \sqrt{\frac{\cos^6\lambda_m}{\sqrt{1+3\sin^2\lambda_m}}} = \frac{\cos^3\lambda_m}{(1+3\sin^2\lambda_m)^{1/4}} $$

where \( \lambda_m \) is the magnetic latitude of the particle’s mirror point. The plot below illustrates this relationship.

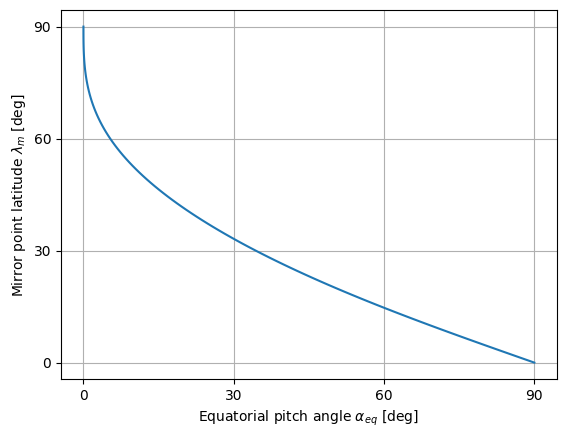
From this plot, it is evident that particles with smaller equatorial pitch angles have higher mirror point latitudes, meaning they reflect closer to the magnetic poles and can travel farther toward the poles. This occurs because the pitch angle \( \tan\alpha = v_\perp/v_\parallel \), i.e., the angle is inversely proportional to the parallel velocity of the particle. A smaller pitch angle implies a higher parallel velocity, allowing the particle to travel further along the field line. Note that for angles between \( 0^\circ \) and \( 90^\circ \), \( \tan\alpha \propto \alpha \), i.e., the tangent of the angle is approximately proportional to the angle. The plot also shows that particles with larger equatorial pitch angles have lower mirror point latitudes, reflecting before reaching closer to the poles. Not all particles can travel to the same latitude.

The time taken by a particle, starting from the equatorial plane, to bounce from the northern pole to the southern pole and return to the equator is called the bounce period \( \tau_b \). It can be determined through integration using the definition of velocity. If the parallel velocity is \( v_\parallel = ds/d\tau \), then:

$$ \tau = 4\int_0^{\lambda_m} \frac{ds}{v_\parallel} = 4\int_0^{\lambda_m} \frac{ds}{d\lambda} \frac{d\lambda}{v_\parallel} $$

The integral is multiplied by 4 because the particle traverses the distance \( \lambda_m \) four times in one period.

$$ v_\parallel^2 = v^2-v_\perp^2 = v^2(1-\sin^2\alpha) \Rightarrow v_\parallel = v\sqrt{1-(B/B_{eq})\sin^2\alpha_{eq}} $$

Substituting the expression for parallel velocity and the full form of \( ds/d\lambda \) into the equation results in a large integral, which can be numerically solved to give an approximate value:

$$ \tau_b \approx 4\frac{r_{eq}}{v}(1.30-0.56\sin\alpha_{eq}) = \frac{LR_E}{\sqrt{W/m}} (3.7-1.6\sin\alpha_{eq}) $$

where \( L = r_{eq}/R_E \) and the kinetic energy \( W = mv^2/2 \) is used. For electrons and protons with 1 keV energy gyrating at a \( 45^\circ \) pitch angle, this equation is plotted below.

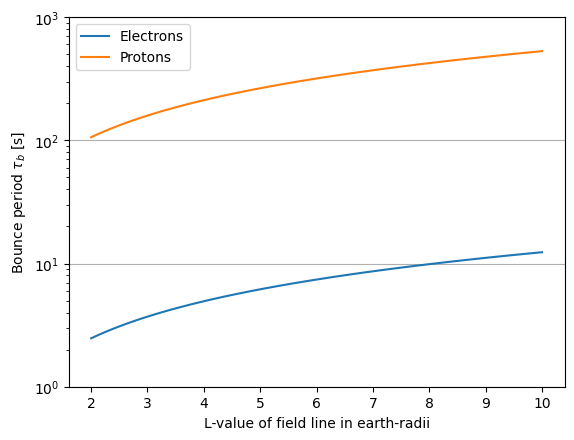
Because electrons are lighter, their bounce period is only a few seconds, whereas that for protons or ions can be several minutes. Longitudinal invariance is maintained only when the frequency of changes in the plasma is much lower than the bounce frequency, meaning the periods of these changes (inverse of frequency) must be much greater than the bounce period. For electrons, the shorter bounce period ensures no issues with longitudinal invariance, but for protons and ions, some adiabatic invariants may no longer hold.

Even if the longitudinal invariant remains constant, not all particles may remain trapped along the magnetic field lines. If a particle’s mirror point descends deep into the Earth’s atmosphere, it may be absorbed due to interactions with neutral particles, resulting in the ionized particle being lost. To account for this, an ‘equatorial loss cone’ \( \alpha_l \) is defined as:

$$ \sin^2\alpha_l = \frac{B_{eq}}{B_E} = \frac{\cos^6\lambda_E}{\sqrt{1+3\sin^2\lambda_E}} $$

where \( B_E \) is the magnetic field at the Earth’s surface, and \( \lambda_E \) is the magnetic latitude where a field line touches the Earth’s surface. Particles are absorbed approximately at an altitude of 100 km, but since the magnetic field strength at the surface and at 100 km altitude differ only slightly, the surface value is used here.

If the equatorial pitch angle is smaller than \( \alpha_l \), the particle’s gyration will take it so deep into the atmosphere that it will be absorbed. All particles within the solid angle \( d\Omega \) shown above will be lost. Using the equation above, the loss cone can be expressed in terms of the L-value, recalling that \( \cos^2\lambda_E = L^{-1} \):

$$ \sin\alpha_l = (4L^6-3L^5)^{-1/4} $$

This relationship is shown in the plot below.

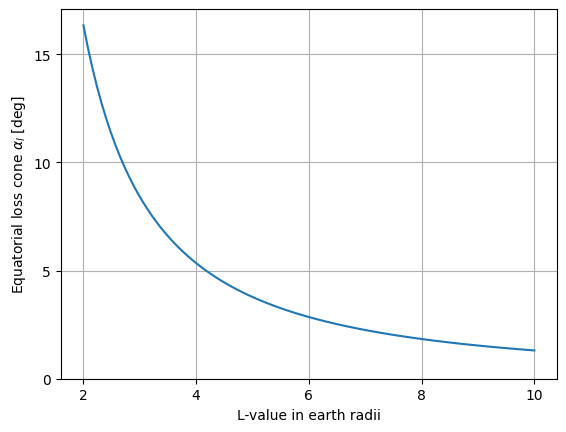
Thus, the width of the loss cone depends only on the L-value, which corresponds to the equatorial radius of a field line relative to the Earth’s radius. For distant field lines, the loss cone becomes very narrow. At geostationary orbit, approximately 6.6 Earth radii, the loss cone width is only 3°.