- English
- বাংলা
Table of Contents
VII. Magnetic force and field
1. Magnetism
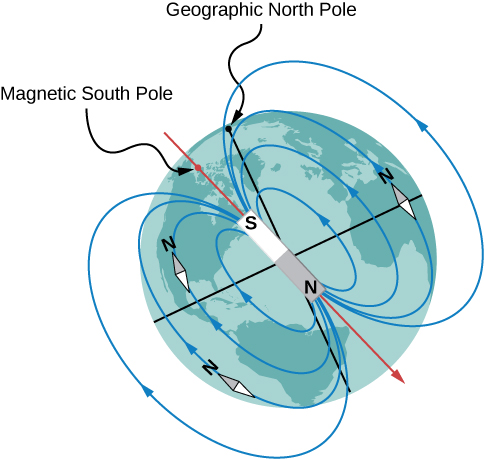
2. Magnetic fields and lines
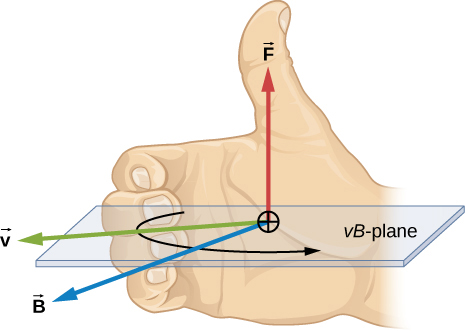
Magnetic field is defined using the magnetic force a charged particle experiences while moving in that field:
$$ \vec{F} = q \vec{v} \times \vec{B} = qvB\sin\theta $$
where $\vec{v}$ is the velocity of the particle, $\vec{B}$ is the magnetic field, and $\theta$ the angle between the two.
SI unit is tesla (T), and another unit is gauss (G). 1 G = $10^{-4}$ T.
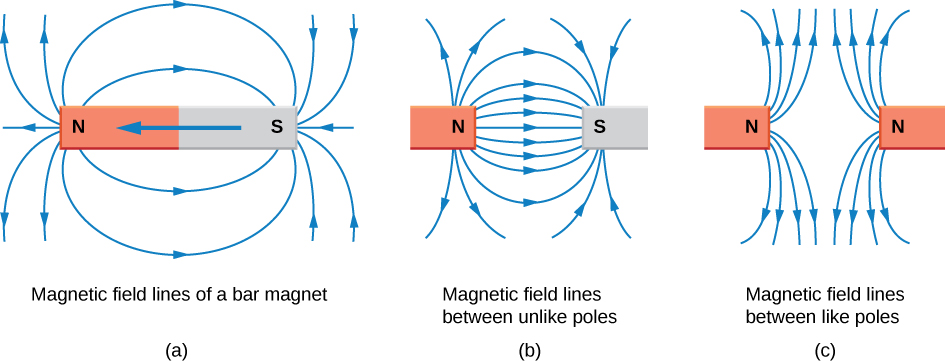
3. Motion of a charged particle in B-field
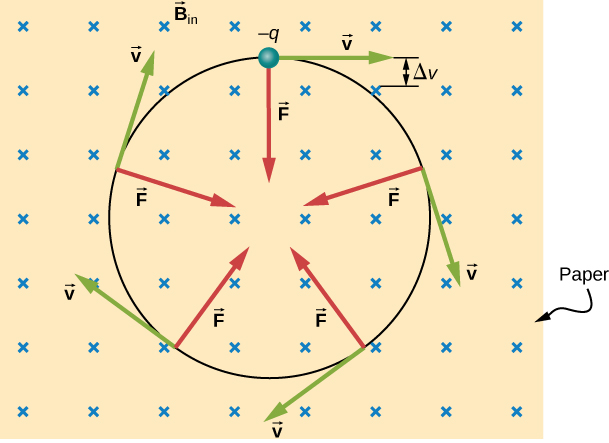
$$ F = qvB \Rightarrow \frac{mv^2}{r}=qvB \Rightarrow r = \frac{mv}{qB} $$
which is the radius of the curvature of the path of a negative charge. The period
$$ T = \frac{2\pi r}{v} = \frac{2\pi m}{qB}. $$
If the velocity is not perpendicular to the field, then we have a helical motion.
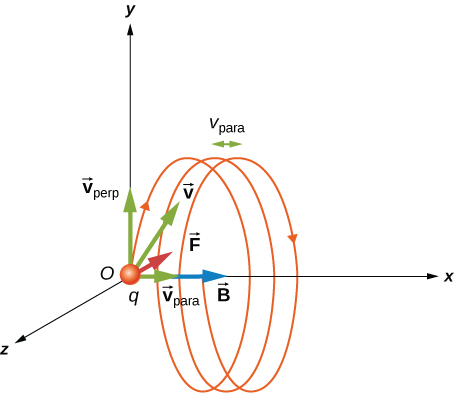
The $v_{perp}=v\sin\theta$ provides the circular motion and $v_{para}=v\cos\theta$ provides the forward motion resulting in a pitch $p=v_{para}T$.
4. Magnetic force on a current-carrying conductor
Electric current $I=neAv_d$.

The magnetic force on a single charge is $e\vec{v}_d\times \vec{B}$. Total force on charges within the volume $nAdl$ would then be
$$ d\vec{F} = nAdle \vec{v}_d\times \vec{B}. $$
If $d\vec{l}$ is a vector pointing in the direction of $\vec{v}_d$, then
$$ d\vec{F} = neAv_d d\vec{l}\times \vec{B} = I d\vec{l} \times \vec{B}. $$
If the wire is straight and the field is uniform,
$$ \vec{F} = I \vec{l} \times \vec{B}. $$
5. Force and torque on a current loop
Apply $\vec{F} = I\vec{l}\times \vec{B}$ on 4 sides.
$$ \vec{F}_1 = IaB \sin(90^\circ-\theta)\hat{i} = IaB\cos\theta\hat{i} $$
$$ \vec{F}_3 = - IaB \sin(90^\circ+\theta)\hat{i} = - IaB\cos\theta\hat{i} $$
$$ \vec{F}_2 = IbB \hat{k} $$
$$ \vec{F}_4 = - IbB \hat{k} $$
$$ \sum \vec{F} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + \vec{F}_4 = 0 $$
But the net torque is not zero.
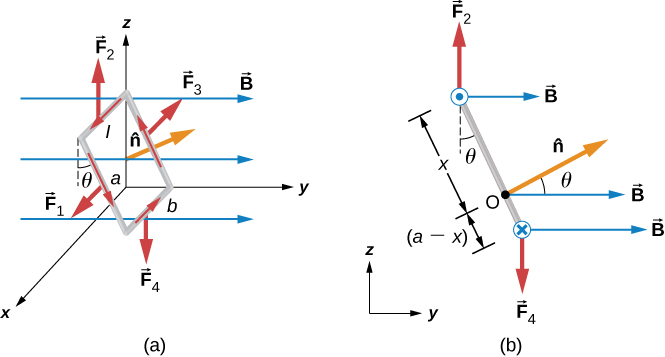
$$ \sum \vec{\tau} = \vec{\tau}_2 + \vec{\tau}_4 = F_2x\sin\theta\hat{i} - F_4(a-x)\sin\theta\hat{i} = -IabB\sin\theta\hat{i} = - IAB\sin\theta\hat{i} $$
Define magnetic dipole moment as $\vec{\mu} = NIA\hat{n} $ and write
$$ \vec{\tau} = \vec{\mu} \times \vec{B}. $$
And potential energy for a magnetic dipole $U=-\vec{\mu} \cdot \vec{B}$.
