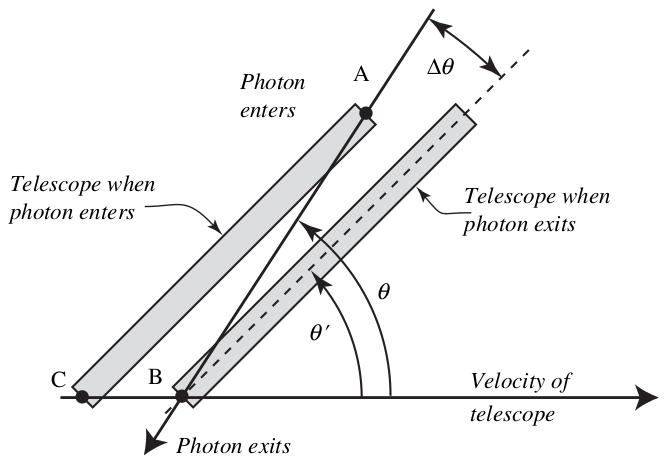
In this example of 2D frame moving only in the $x$-direction

$$ \tan\phi = \frac{c_y'}{c_x'} = \frac{c_y}{\gamma(c_x+v)} $$

where $\gamma=(1-v^2/c^2)^{-1/2}$ and $v$ is the velocity of the observer. The velocity components of light in the rest and moving frame are $(c_x,c_y)$ and $(c_x',c_y')$, respectively. So

$$ \tan\phi = \frac{c\sin\theta}{\gamma(c\cos\theta+v)} = \frac{\sin\theta}{\gamma(v/c+\cos\theta)}. $$

If $v \ll c$, $\gamma=1$. and if $\theta=90^\circ$ then

$$ \tan(\theta-\phi) = \cot\phi = \frac{\gamma(v/c+\cos\theta)}{\sin\theta} = \frac{v}{c} $$

and, finally, if $\theta-\phi$ is very small then aberration $\alpha = \theta-\phi \approx v/c$.