- English
- বাংলা
Table of Contents
Questions and Problems
1. One dimension
1.1 Velocity
(A) Define and derive instantaneous velocity from average velocity using equations and a diagram.
(B) The position of a particle is given by $x(t)=3t+0.5t^3$ m. Calculate its instantaneous velocity at $t=2$ s and its average velocity between 1 s and 3 s.
(A) Follow Section 2 of the theory notes.
(B) Use Example 3.3 in the Textbook.
1.2 Acceleration
(A) Define and derive instantaneous acceleration from average acceleration using equations and a diagram.
(B) The velocity of a moving particle is given by $v(t)=20t-5t^2$ m/s. Calculate its instantaneous acceleration at $t=2$ s and its average acceleration between 1 s and 3 s.
(A) Follow Section 3 of the theory notes.
(B) Use Example 3.6 in the Textbook.
1.3 Position, velocity, acceleration
(A) If the position of a particle is $x=\sin(t)$ m, what are the functional forms of the velocity $v(t)$ and acceleration $a(t)$? Show the relationships among position, velocity and acceleration using a diagram.
(B) If the position of a particle is given by $x(t)=5t^3-7t^2+9$ m, what are the functional forms of the velocity and acceleration? Calculate the position, velocity and acceleration at 5 s.
(A) Follow Section 4. Note that the first derivative is related to slope and second derivative to curvature.
(B) Differentiate $x(t)$ once to get velocity $v(t)$ and twice to get acceleration $a(t)$. Then calculate $x,v,a$ when $t=5$ s.
1.4 Displacement from acceleration
(A) Show that the displacement of an object $s=x-x_0=v_0+at^2/2$ when acceleration $a$ is constant.
(B) Dragsters (pictured below) can achieve an average acceleration of $26.0$ m/s$^2$. Suppose a dragster accelerates from rest at this rate for 5.56 s. How far does it travel in this time?

(A) Follow Section 5.
(B) Use Example 3.8 in the textbook.
1.5 Velocity from displacement
(A) Show that the final velocity of an object $v^2=v_0^2+2a(x-x_0)$ when acceleration $a$ is constant.
(B) Calculate the final velocity of the dragster shown in the previous example.
(A) Follow Section 5.
(B) Use Example 3.9.
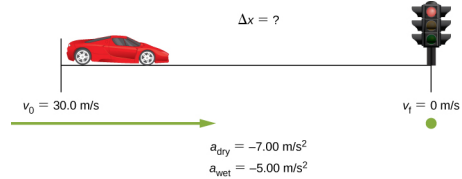
1.6 Stopping a car
On dry concrete, a car can decelerate at a rate of $7.00$ m/s$^2$, whereas on wet concrete it can decelerate at only $5.00$ m/s$^2$.
(A) Find the distances necessary to stop a car moving at $30.0$ m/s dry concrete and on wet concrete.
(B) Repeat both calculations and find the displacement from the point where the driver sees a traffic light turn red, taking into account his reaction time of $0.500$ s to get his foot on the brake.
Use Example 3.10.
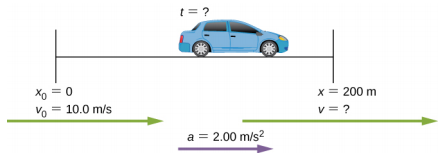
1.7 Ramp to a highway
(A) Suppose a car merges into highway traffic on a 200-m-long ramp. If its initial velocity is $10.0$ m/s and it accelerates at $2.00$ m/s$^2$, how long does it take the car to travel the $200$ m up the ramp?
(B) Which of the two solutions of the quadratic equation in this case is meaningful and why?
Use Example 3.11.
1.8 Spaceship
(A) A spaceship has left Earth’s orbit and is on its way to the Moon. It accelerates at $20$ m/s$^2$ for $2$ min and covers a distance of $1000$ km. What are the initial and final velocities of the spaceship?
(B) Which of the two solutions of the quadratic equation in this case is meaningful and why?
Use Example 3.12.
1.9 Cheetah and Gazelle
A cheetah waits in hiding behind a bush. The cheetah spots a gazelle running past at $10$ m/s. At the instant the gazelle passes the cheetah, the cheetah accelerates from rest at $4$ m/s2 to catch the gazelle.
(A) How long does it take the cheetah to catch the gazelle?
(B) What is the displacement of the gazelle and cheetah?
Use Example 3.13.
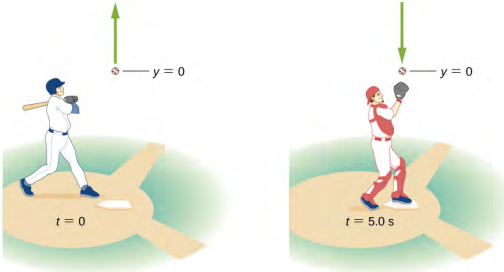
1.10 Baseball at free-fall
A batter hits a baseball straight upward and the ball is caught $5.0$ s after it is struck. Assume the ball is hit and caught at the same location.
(A) What is the initial velocity of the ball? What is the maximum height the ball reaches? How long does it take to reach the maximum height?
(B) What is the acceleration at the top of its path? What is the velocity of the ball when it is caught?
Use Example 3.15.
1.11 Velocity from acceleration
A motorboat is traveling at a constant velocity of $5.0$ m/s when it starts to decelerate to arrive at the dock. Its acceleration is $a(t) = −14 t$ m/s$^2$.
(A) What is the velocity function of the motorboat? And at what time does the velocity reach zero?
(B) What is the position function of the motorboat? And what is the displacement of the motorboat from the time it begins to decelerate to when the velocity is zero?
[Use diagrams to show how position is calculated from velocity and velocity is calculated from acceleration.]
Use Example 3.17.
2. Two dimensions
2.1 Polar orbiting satellite
(A) How can you represent a 2D vector using its two components geometrically (diagrams) and algebraically (equations)?
(B) A satellite is in a circular polar orbit around Earth at an altitude of $400$ km—meaning, it passes directly overhead at the North and South Poles. What is the magnitude and direction of the displacement vector from when it is directly over the North Pole to when it is at $−45^\circ$ latitude?
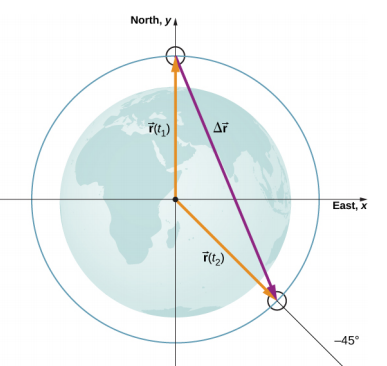
Follow Chapter 1, Section 4.2.1.
Us Example 4.1 in textbook.
2.2 Velocity in 2D
The position function of a particle is $\mathbf{r}(t) = 2t^2 \hat{i} + (2+3t) \hat{j} + 5t \hat{k} m.
(A) What is the instantaneous velocity and speed at t = 2.0 s?
(B) What is the average velocity between 1.0 s and 3.0 s?
Use Example 4.3.
2.3 Acceleration in 2D
A particle has a position function $\overrightarrow{r}(t)=(10t-t^2)\hat{i}+5t\hat{j}+5t\hat{k}$ m.
(A) What are the velocity and acceleration functions of the particle?
(B) Describe the position, velocity and acceleration of the particle at time $t=0$ s.
Use Example 4.5.
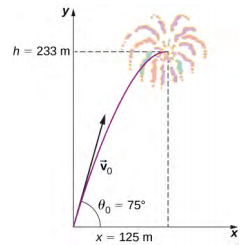
2.4 Fireworks
During a fireworks display, a shell is shot into the air with an initial speed of $70.0$ m/s at an angle of $75.0^\circ$ above the horizontal, as illustrated in the figure below. The fuse is timed to ignite the shell just as it reaches its highest point above the ground.
(A) Calculate the height at which the shell explodes. How much time passes between the launch of the shell and the explosion?
(B) What is the horizontal displacement of the shell when it explodes? What is the total displacement from the point of launch to the highest point?